Question

What is the remainder when 3x^4 +2x^3-x^2+2x-24)/(x+2)

Answer 1

remainder = 0

Explanation:

Using the Remainder Theorem

Given f(x) divided by (x + h) then the remainder is found by evaluating f(- h)

Here the divisor is (x + 2), hence evaluate at h = - 2

Let f(x) = 3
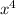`x^(4)` + 2x³ - x² + 2x - 24, then

f(- 2) = 3
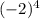`(-2)^(4)` + 2(- 2)³ - (- 2)² + 2(- 2) - 24

= 3(16) + 2(- 8) - 4 - 4 - 24

= 48 - 16 - 4 - 4 - 24 = 0 ← Remainder

Remainder = 0 , hence (x + 2) is a factor of f(x)