Question

Prove that the diagonals of a parallelogram bisect each other.

Plan: Since midpoints will be involved, use multiples of __ to name the coordinates for B, C, and D.

Answer 1

2

Explanation:

The diagonals of a parallelogram bisect each other. Since midpoints will be involved, use multiples of 2 to name the coordinates for B, C, and D.

Answer 2

2

Explanation:

Well by definition a Rhombus is an equilateral paralelogram, AB =BC=CD=DA with all congruent sides, and Diagonals with different sizes.

Also a midpoint is the mean of coordinates, like E is the mean coordinate of A,C, and B, D

`(B+D)/(2)=E\\  \\ B+D=2E\\ and\\\\  (A+C)/(2) =E\\ A+C=2E`

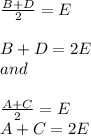
So the sum of the Coordinates B and D over two returns the midpoint.

And subsequently the sum of the Coordinates B +D equals twice the E coordinates. The same for the sum: A +C

Given to the fact that both halves of those diagonals coincide on E despite those diagonals have different sizes make us conclude, both bisect each other.