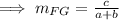Question

Prove that the segments joining the midpoint of consecutive sides of an isosceles trapezoid form a rhombus.

Find the slope of DE and FG.

Answer 1

See explanation

Explanation:

a) To prove that DEFG is a rhombus, it is sufficient to prove that:

1. All the sides of the rhombus are congruent:
   `|DG|\cong |GF| \cong |EF| \cong |DE|`
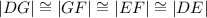
2. The diagonals are perpendicular

Using the distance formula;
`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`|DG|=√((0-(-a-b))^2+(0-c)^2)`

`\implies |DG|=√(a^2+b^2+c^2+2ab)`

`|GF|=√(((a+b)-0)^2+(c-0)^2)`

`\implies |GF|=√(a^2+b^2+c^2+2ab)`

`|EF|=√(((a+b)-0)^2+(c-2c)^2)`

`\implies |EF|=√(a^2+b^2+c^2+2ab)`

`|DE|=√((0-(-a-b))^2+(2c-c)^2)`

`\implies |DE|=√(a^2+b^2+c^2+2ab)`

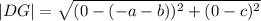
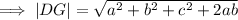
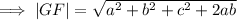
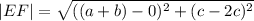
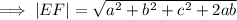
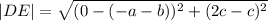
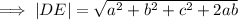
Using the slope formula;
`m=(y_2-y_1)/(x_2-x_1)`

The slope of EG is
`m_(EG)=(2c-0)/(0-0)`

`\implies m_(EG)=(2c)/(0)`

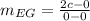
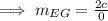
The slope of EG is undefined hence it is a vertical line.

The slope of DF is
`m_(DF)=(c-c)/(a+b-(-a-b))`

`\implies m_(DF)=(0)/(2a+2b))=0`

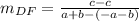
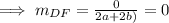
The slope of DF is zero, hence it is a horizontal line.

A horizontal line meets a vertical line at 90 degrees.

Conclusion:

Since
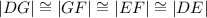`|DG|\cong |GF| \cong |EF| \cong |DE|` and
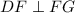`DF \perp FG` , DEFG is a rhombus

b) Using the slope formula:

The slope of DE is
`m_(DE)=(2c-c)/(0-(-a-b))`

`m_(DE)=(c)/(a+b))`

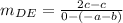
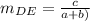
The slope of FG is
`m_(FG)=(c-0)/(a+b-0)`

`\implies m_(FG)=(c)/(a+b)`