Answer:
m=7
Remainder =4
If q=1 then r=3 or r=-1.
If q=2 then r=3.
They are probably looking for q=1 and r=3 because the other combinations were used earlier in the problem.
Explanation:
Let's assume the remainders left when doing P divided by (x-1) and P divided by (2x+3) is R.
By remainder theorem we have that:
P(1)=R
P(-3/2)=R
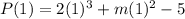
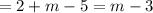
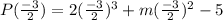

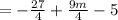
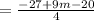
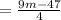
Both of these are equal to R.
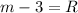
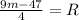
I'm going to substitute second R which is (9m-47)/4 in place of first R.
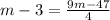
Multiply both sides by 4:

Distribute:
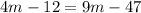
Subtract 4m on both sides:
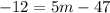
Add 47 on both sides:
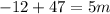
Simplify left hand side:
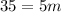
Divide both sides by 5:
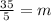
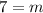
So the value for m is 7.
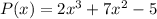
What is the remainder when dividing P by (x-1) or (2x+3)?
Well recall that we said m-3=R which means r=m-3=7-3=4.
So the remainder is 4 when dividing P by (x-1) or (2x+3).
Now P divided by (qx+r) will also give the same remainder R=4.
So by remainder theorem we have that P(-r/q)=4.
Let's plug this in:
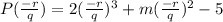
Let x=-r/q
This is equal to 4 so we have this equation:

Subtract 4 on both sides:
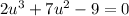
I see one obvious solution of 1.
I seen this because I see 2+7-9 is 0.
u=1 would do that.
Let's see if we can find any other real solutions.
Dividing:
1 | 2 7 0 -9
| 2 9 9
-----------------------
2 9 9 0
This gives us the quadratic equation to solve:
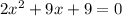
Compare this to

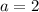

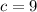
Since the coefficient of
 is not 1, we have to find two numbers that multiply to be
is not 1, we have to find two numbers that multiply to be
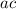 and add up to be
and add up to be
 .
.
Those numbers are 6 and 3 because
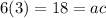 while
while
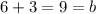 .
.
So we are going to replace
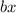 or
or
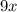 with
with
 then factor by grouping:
then factor by grouping:


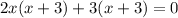
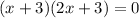
This means x+3=0 or 2x+3=0.
We need to solve both of these:
x+3=0
Subtract 3 on both sides:
x=-3
----
2x+3=0
Subtract 3 on both sides:
2x=-3
Divide both sides by 2:
x=-3/2
So the solutions to P(x)=4:
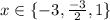
If x=-3 is a solution then (x+3) is a factor that you can divide P by to get remainder 4.
If x=-3/2 is a solution then (2x+3) is a factor that you can divide P by to get remainder 4.
If x=1 is a solution then (x-1) is a factor that you can divide P by to get remainder 4.
Compare (qx+r) to (x+3); we see one possibility for (q,r)=(1,3).
Compare (qx+r) to (2x+3); we see another possibility is (q,r)=(2,3).
Compare (qx+r) to (x-1); we see another possibility is (q,r)=(1,-1).