Question

Find all solutions of each equation on the interval 0 ≤ x < 2 pi.

tan^2 x sec^2 x +2 sec^2 x - tan^2 x=2
SOMEONE PLEASE HELPPP!!

Answer 1

`x = 0 , \pi , 2\pi`

Explanation:

The given equation is:l

`\tan^(2) (x) \sec^(2) x + 2 \sec^(2) x - \tan^(2) x = 2`

Add -2 to both sides of the equation to get:

`\tan^(2) (x) \sec^(2) x + 2 \sec^(2) x - \tan^(2) x - 2 = 0`

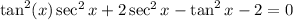
We factor the LHS by grouping.

`\sec^(2) x(\tan^(2) (x) + 2 ) - 1( \tan^(2) x + 2) = 0`

`(\sec^(2) x - 1)(\tan^(2) (x) + 2)= 0`

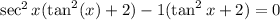
We now apply the zero product property to get:

`(\sec^(2) x - 1) = 0 \: \: or \: \: (\tan^(2) (x) + 2)= 0`

This implies that:

`\sec^(2) x = 1 \: \: or \: \: \tan^(2) (x) = - 2`

`\tan^(2) (x) = - 2 \implies \tan(x) = \pm √( - 2)`

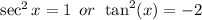
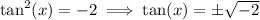
This factor is never equal to zero and has no real solution.

`\sec^(2) x = 1`

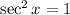
This implies that:

`\sec \: x= \pm√(1)`

`\sec(x) = \pm - 1`

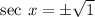
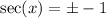
Recall that

`(1)/( \sec(x) ) = \cos(x)`

We reciprocate both sides to get:

`\cos(x) = \pm1`

`\cos x = 1 \: or \: \cos x = - 1`

`\cos x = 1 \implies \: x = 0 \: or \: 2\pi`

`\cos x = - 1 \implies \: x = \pi`

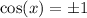
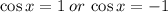
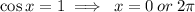
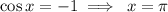
Therefore on the interval

`0 \leqslant x \leqslant 2\pi`

`x = 0 , \pi , 2\pi`