Question

What is the value of X?

Answer 1

x = 7

Step-by-step explanation:

Because 25 is a perfect square of 5, we can turn

`5^(3x - 5)` =
`25^(x + 1)`

into

`5^(3x - 5)` =
`5^(2x + 2)`

Since the bases are now both equal, we can completely ignore them, as we are only trying to find x. This leaves us with:

3x - 5 = 2x + 2

All we have to do now is solve for x:

x - 5 = 2 Subtract 2x from both sides.

x = 7 Add 5 to both sides.

Hope this helps! :)

Answer 2

x = 7

Step-by-step explanation:

To solve for x in this equation, we're going to need to get the two exponents (3x - 5 and x + 1) equal to each other, but we can't do that unless our bases are the same.

For example, in
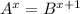`A^(x) = B^(x + 1)`, you cannot solve x = x + 1. In
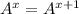`A^(x) = A^(x + 1)`, you can solve x = x + 1.

Just by looking at the bases, 5 and 25, you can tell that it will be simple to make them match. 25 is just 5². The tricky part is going to be figuring out where to put the 2 into x + 1.

Let's look at another example. If you have
`2^(2 * 2)`, then you can simplify it to
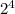`2^(4)`, which is 16. Or, you could do them one at a time, so
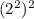`(2^(2)) ^(2)`. This way you'd have 4², which you'd be able to recognize as 16. Based on this example, we know that to make our bases the same, we need to change
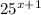`25^(x + 1)` to
`5^(2(x + 1))`.

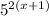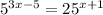`5^(3x-5) = 25^(x+1)` Change the right side to
`5^(2(x + 1))`

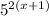
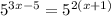`5^(3x-5) = 5^(2(x+1))` Simplify that exponent using distribution

`5^(3x-5) = 5^(2x+2)`

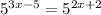
Now that the bases match, you can get rid of them and just set the exponents equal to each other and solve for x.

3x - 5 = 2x + 2 Add 5 to both sides

3x = 2x + 7 Subtract 2x from both sides

x = 7

Now, check you work!

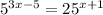`5^(3x-5) = 25^(x+1)` Plug in 7 for x

`5^(3(7)-5) = 25^((7)+1)` Simplify

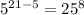`5^(21-5) = 25^(8)` Simplify one more time

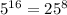`5^(16) = 25^(8)` Plug these into a calculator if you have one

152587890625 = 152587890625 So you know that x = 7 is correct.