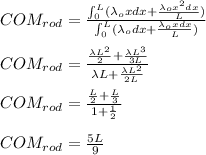Question

Determine the CM of a rod assuming its linear mass density λ (its mass per unit length) varies linearly from λ = λ0 at the left end to double that value, λ = 2λ0

Answer 1

Center Of Mass lies at 5L/9 from O as shown.

Step-by-step explanation:

The Center of mass of any object is given by

`X_(com)=(\int xdm)/(\int dm)\\\\Y_(com)=(\int ydm)/(\int dm)`

where (x,y) is location of point with mass dm

Now since rod is a linear object we have it's y co-ordinates as zero

Thus

`COM_(rod)=(\int xdm)/(\int dm)\\\\`

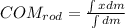
The mass of an element 'dx' at a distance 'x' from O can be written as

`dm=\lambda(x) dx\\\\\lambda(x) ={\lambda _0}+(2\lambda _(0)-\lambda _(0))/(L)x\\\\\lambda (x)=\lambda _0+(\lambda _0)/(L)x`

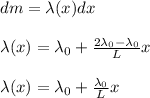
Thus we have

`dm=\lambda(x) dx\\\\\lambda(x) ={\lambda _0}+(2\lambda _(0)-\lambda _(0))/(L)x\\\\\lambda (x)=\lambda _0+(\lambda _0)/(L)x\\\\COM_(rod)=(\int x\lambda(x)dx)/(\int \lambda(x)dx)\\\\=(\int (\lambda_(0)+\lambda_(0)(x)/(L))xdx)/(\int (\lambda_(o)+\lambda_O(x)/(L))dx)`

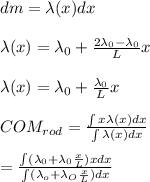
Solving with limits form (0,L) we get

`COM_(rod)=(\int_(0)^(L)(\lambda_(o)xdx+(\lambda_(o)x^(2)dx)/(L)))/(\int_(0)^(L)(\lambda_(o)dx+(\lambda_(o)xdx)/(L)))\\\\COM_(rod)=((\lambda L^(2))/(2)+(\lambda L^(3))/(3L))/(\lambda L+(\lambda L^(2))/(2L))\\\\COM_(rod)=((L)/(2)+(L)/(3))/(1+(1)/(2))\\\\COM_(rod)=(5L)/(9)`