Question

If f(x)=(x+3)³+4
let g(x)=f(x+1)-2
find when g(x)=12

Answer 1

`x=\sqrt[3]{10}-2`

Explanation:

The composite function (f(x+1)) is moved in the x-axis by -1, you know this by solving x+1=0.

The equivalent expresion for f(x+1) is

`f(x+1)= (x-1+3)^(3)+4`

`f(x+1)=(x+2)^(3)+ 4`

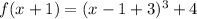
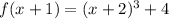
Eval the above expression in g(x)

`g(x)=(x+2)^(3)+4-2`

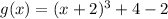
We must find x that gives g(x)=12

The equation is the following

`12=(x+2)^(3)+2`

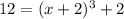
Grouping terms>

`(x+2)^(3) =10`

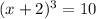
To solve for x, must apply cubic root in both sides of equation:

`\sqrt[3]{(x+2)^(3) } =\sqrt[3]{10}`

it then turns in the following>

`x+2=\sqrt[3]{10}\\`

Giving the stated answer