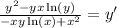Question

X^y=y^x find derivitive

Answer 1

`y'=(y^2-xy\ln(y))/(x^2-xy\ln(x))`

Explanation:

Take natural log of both sides first.

`x^y=y^x`

`\ln(x^y)=\ln(y^x)`

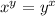
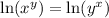
Taking the natural log of both sides allows you to bring down the powers.

`y\ln(x)=x\ln(y)`

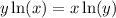
I'm going to differentiate both sides using the power rule.

`(y)'(\ln(x))+(\ln(x))'y=(x)'(\ln(y))+(\ln(y))'x`

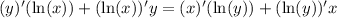
Now recall (ln(x))'=(x)'/x=1/x while (ln(y))'=(y)'/y=y'/y.

`y'(\ln(x))+(1)/(x)y=1(\ln(y))+(y')/(y)x`

Simplifying a bit:

`y' \ln(x)+(y)/(x)=\ln(y)+(y')/(y)x`

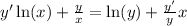
Now going to gather my terms with y' on one side while gathering other terms without y' on the opposing side.

Subtracting y'ln(x) and ln(y) on both sides gives:

`(y)/(x)-\ln(y)=-y'\ln(x)+(y')/(y)x`

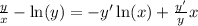
Now I'm going to factor out the y' on the right hand side:

`(y)/(x)-\ln(y)=(-\ln(x)+(x)/(y))y'`

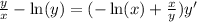
Now we get to get y' by itself by dividing both sides by (-ln(x)+x/y):

`((y)/(x)-\ln(y))/(-\ln(x)+(x)/(y))=y'`

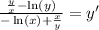
Now this looks nasty to write mini-fractions inside a bigger fraction.

So we are going to multiply top and bottom by xy giving us:

`(y^2-yx\ln(y))/(-xy\ln(x)+x^2)=y'`

`y'=(y^2-xy\ln(y))/(x^2-xy\ln(x))`