Answer:
a.
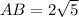
b.
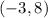
c.
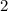
Explanation:
You have the points:
A(-2,10)
where i will call:
 and
and
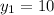
B(-4,6)
where i will call:
 and
and
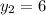
for our calculations we are going to need the distance in x between the points (
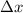 )and the distance in y between the points (
)and the distance in y between the points (
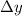 ):
):
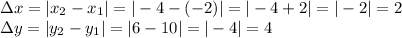
a. To find AB (the distance between point A and point B) you need The Pythagorean Theorem:
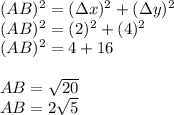
b. to find the coordinates of the midpoint we average the x-coordinates and the y coordinates
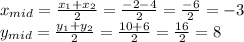
so the midpoint
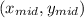 is at:
is at:
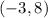
c. For the slope we use the slope formula:
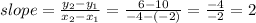
The slope is equal to 2.