Answer:
First Image:
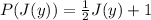
Explanation:
We have the following functions:
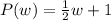
Here, P(w) represents the number of paintings Jenny completes in w weeks.
J(y) = Number of weeks per year.
Since, J(y) is the number of weeks spent per year in painting, in order to calculate the paintings completed in a year we substitute w = J(y) in the above equation. So the equation becomes:
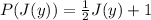
This composite function would represent number of paintings Jenny completes in a year.