Question

A manufacturing company sells its products directly to customers and operates 5 days a week, 52 weeks a year. The production department of this company can produce at the rate of 60 units per day. The setup cost for a production run is $ 125.00. The cost of holding is $ 4.00 per unit per year. The demand for the item is continuous and constant and is 3,900 units per year. (Note: The demand occurs only when the company is operating, that is, 5 days a week for 52 weeks). Find the optimum number of units to be produced in one batch.

Answer 1

Optimum number per batch 494

Step-by-step explanation:

EOQ minimize the cost for both, setup and holding.

`Q_(opt) = \sqrt{(2DS)/(H)}`

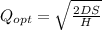
How to Remember:

Demand per year and order cost goes in the dividend.

Holding cost goes in the divisor.

demand 3,900

setup cost 125

holding 4

`Q_(opt) = \sqrt{(2* 3,900 \: times 125)/(4)}`

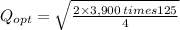
493.71 = 494