Answer:
Velocity of the car decreases.
Step-by-step explanation:
We can understand the situation if we apply the conservation of energy principle to the situation
Let the initial mass of the freight be
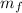
Initial velocity of the freight be
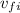
Thus the initial Kinetic energy of the freight will be

When a Coal Block of mass M falls into the freight it's energy will become

Equating both the energies we get final velocity as
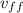
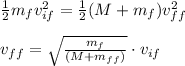
As we see that
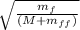 is less than 1 we can infer that velocity decreases.
is less than 1 we can infer that velocity decreases.