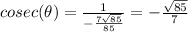Question

Suppose θ is an angle in the standard position whose terminal side is in Quadrant IV and cot θ= -6/7 . Find the exact values of the five remaining trigonometric functions of θ. Show your work

Answer 1

`tan(\theta)=-(7)/(6)`

`sec(\theta)=(√(85) )/(6)`

`cos(\theta)=(6√(85) )/(85)`

`sin(\theta)=-(7√(85))/(85)`

`cosec(\theta)=-(√(85))/(7)`

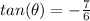
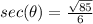
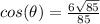
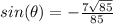
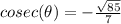
Explanation:

`cot (\theta) = -(6)/(7)`

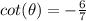
a) Since,

`tan(\theta) = (1)/(cot(\theta))`

`tan(\theta) = (1)/(-(6)/(7) )=-(7)/(6)`

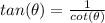
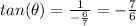
b) Also, according to the Pythagorean identity:

`sec^(2)(\theta)=1+tan^(2)(\theta)`

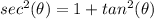
Using the value of tan(
`\theta`), we get:

`sec^(2)(\theta)=1+(-(7)/(6) )^(2)\\\\ sec^(2)(\theta)=(85)/(36)\\\\ sec(\theta)=\pm \sqrt{(85)/(36) } \\\\ sec(\theta)=\pm (√(85) )/(6)`

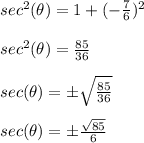
Since, secant is positive in 4th quadrant, we will only consider the positive value. i.e.

`sec(\theta)=(√(85) )/(6)`

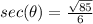
c) Since,

`cos(\theta)=(1)/(sec(\theta))`

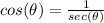
Using the value of secant, we get:

`cos(\theta)=(1)/((√(85) )/(6) ) =(6√(85) )/(85)`

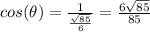
d) According to Pythagorean identity:

`sin^(2)(\theta)=1-cos^(2)(\theta)\\sin(\theta)=\pm \sqrt{1-cos^(2)(\theta)}`

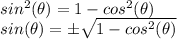
Since, sine is negative in fourth quadrant, we will consider the negative value. Using the value of cosine, we get:

`sin(\theta)=-\sqrt{1-((6√(85) )/(85))^(2)}=-(7√(85))/(85)`

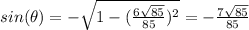
e) Since,

`cosec(\theta)=(1)/(sin(\theta))`

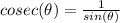
Using the value of sine, we get:

`cosec(\theta)=(1)/(-(7√(85) )/(85))=-(√(85))/(7)`