Question

A block is given an initial velocity of 4.90 m/s up a frictionless 20.5° incline. How far up the incline does the block slide before coming to rest?

Answer 1

7.0 m

Step-by-step explanation:

We can solve the problem by using the work-energy theorem, which states that the work done on the block is equal to the block's change in kinetic energy:

`W=K_f - K_i`

where:

W is the work done (by gravity, since it is the only force acting on the block)

`K_i` is the initial kinetic energy

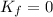`K_f = 0` is the final kinetic energy, which is zero since the block comes to a stop

The work done by gravity against the block is:

`W=-(mgsin \theta) d`

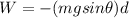
where

m is the mass of the block

g = 9.8 m/s^2 is the acceleration due to gravity

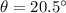`\theta=20.5^(\circ)` is the angle of the incline

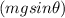`(mg sin \theta)` is the component of the force of gravity that acts along the plane parallel to the incline, and the negative sign is due to the fact that this force acts opposite to the displacement of the block, d

d is the displacement of the block

Instead, the initial kinetic energy is

`K_i = (1)/(2)mv^2`

where

v = 4.90 m/s is the initial speed of the block

Substituting everything into the first equation, we can solve to find d, the displacement covered by the block up the incline:

`-mgsin \theta d = -(1)/(2)mv^2\\d = (v^2)/(g sin \theta)=((4.90)^2)/((9.8)(sin 20.5^(\circ)))=7.0 m`