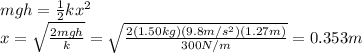Question

A 1.50 kg object is held 1.27 m above a relaxed, massless vertical spring with a force constant of 300 N/m. The object is dropped onto the spring. (a) How far does the object compress the spring?

Answer 1

0.353 m

Step-by-step explanation:

According to the law of conservation of energy, the initial energy that the object possesses (in the form of gravitational potential energy) is converted into elastic potential energy of the spring.

The initial gravitational potential energy of the object is:

`E=mgh`

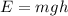
where

m = 1.50 kg is the mass of the object

g = 9.8 m/s^2 is the acceleration of gravity

h = 1.27 m is the height of the object

The final elastic potential energy of the compressed spring is

`E=(1)/(2)kx^2`

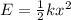
where

k = 300 N/m is the spring constant

x is the compression of the spring

Equalizing the two energies, we find:

`mgh=(1)/(2)kx^2\\x=\sqrt{(2mgh)/(k)}=\sqrt{(2(1.50 kg)(9.8 m/s^2)(1.27 m))/(300 N/m)}=0.353 m`

Answer 2

0.16 m

Step-by-step explanation:

Hello

It is possible to solve this problem using the law of conservation of energy, we know that gravitational potential energy and elastic potential energy must be equal

so

`E_(g) =m*g*h\\\\\\E_(s)=(1)/(2) k x^(2)\\`

`E_(g) =m*g*h=(1)/(2) k x^(2)`

Step 1

define and replace

`E_(g) =m*g*h\\\\Let\\`

m=1.5 kg

h=1.27 m

g=09.81 m/s2

replacing

`E_(g) =m*g*h\\E_(g)=1.5 kg*9.81(m)/(s^(2))*1.27m }\\ E_(g)=25.3098 J`

Step 2

with Eg Known, now we find x (compression of the spring)

`E_(s)=(1)/(2) k x^(2) \\\\x^(2) =(2*E_(s))/(k)\\x=\sqrt{(2*E_(s))/(k)}\\x=\sqrt{(2*25.3095\ J)/( 300 (N)/(m) ) }\\\\x=0.16 m`

x=0.16 m