Question

A ball is thrown upward from a height of 880 feet above the​ ground, with an initial velocity of 96 feet per second. From physics it is known that the velocity at time t is v left parenthesis t right parenthesis equals 96 minus 32 t feet per second. ​a) Find​ s(t), the function giving the height of the ball at time t. ​b) How long will the ball take to reach the​ ground

Answer 1

(a): s(t)= hi + Vo * t - g* t²/2

(b): Will take the ball to reach the ground t= 11 seconds.

Step-by-step explanation:

hi= 880 ft

Vo= 96 ft/s

g= 32 ft/s²

equating to 0 the equation of s(t) and clearing t, we find the time it takes for the ball to fall to the ground.

Answer 2

a)
`s(t) = 96t - 16t^(2) + 880`

b) It will take 11 seconds for the ball to reach the ground.

Step-by-step explanation:

We have an initial height of 880 feet.

And

`v(t) = 96 - 32t`

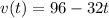
a) Find​ s(t), the function giving the height of the ball at time t

The position, or heigth, is the integrative of the velocity. So

`s(t) = \int {(96 - 32t)} \, dt`

`s(t) = 96t - 16t^(2) + K`

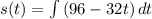
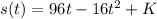
In which the constant of integration K is the initial height, so
`K = 880`

So

`s(t) = 96t - 16t^(2) + 880`

b) How long will the ball take to reach the​ ground

This is t when
`s(t) = 0`

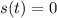
So

`s(t) = -16t^(2) + 96t + 880`

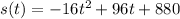
This is t = -5 or t = 11.

However, t is the instant of time, so it has to be a positive value.

So it will take 11 seconds for the ball to reach the ground.