Question

Consider a bridge hand (that is, draw 13 cards at random and without replacement from a regular, 52-card deck). Find the following probabilities: are. Exactly 6 spades, 4 hearts, 2 diamonds, and 1 club

Answer 1

The probability of getting exactly 6 spades,4 hearts,2 diamond and one club=
`\frac{\binom{13}{6}*\binom{13}{4}* \binom{13}{2}*\binom{13}{1}}{\binom{52}{13}}`

Explanation:

We are given that a bridge hand that draw 13 cards at random and without replacement from a regular 52 cards deck.

We have to find the probabilities

1.exactly 6 spades

We know that in one deck

Total number of spades=13

Total number of heart =13

Total number of diamond in a deck=13

Total number of clubs in a deck =13

Total number of cards=52

The probability of getting exactly 6 spades,4 hearts,2 diamond and one club=
`\frac{\binom{13}{6}*\binom{13}{4}*\binom{13}{2}*\binom{13}{1}}{\binom{52}{13}}`

Probability,P(E)=
`(number\;of\;favourable\;cases)/(Total\;number\;of\;cases)`

The probability of getting exactly 6 spades,4 hearts,2 diamond and one club=
`\frac{\binom{13}{6}*\binom{13}{4}* \binom{13}{2}*\binom{13}{1}}{\binom{52}{13}}`

Answer 2

The probability of selecting exactly 6 spades, 4 hearts, 2 diamonds, and 1 club is
`P=(^(13)C_(6)* ^(13)C_(4)* ^(13)C_(2)* ^(13)C_(1))/(^(52)C_(13))`.

Explanation:

Total number of cards in a regular deck of cards = 52

Total number of cards of each suit (spades, hearts, diamonds, club) = 13

Total ways of selecting r cards from total n cards is

`^nC_r=(n!)/(r!(n-r)!)`

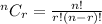
Total ways of selecting 13 cards from total 52 cards is

`\text{Total outcomes}=^(52)C_(13)`

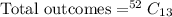
Total ways of selecting exactly 6 spades, 4 hearts, 2 diamonds, and 1 club is

`\text{Favorable outcomes}=^(13)C_(6)* ^(13)C_(4)* ^(13)C_(2)* ^(13)C_(1)`

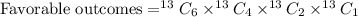
The probability of selecting exactly 6 spades, 4 hearts, 2 diamonds, and 1 club is

`P=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

`P=(^(13)C_(6)* ^(13)C_(4)* ^(13)C_(2)* ^(13)C_(1))/(^(52)C_(13))`

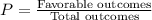
Therefore the probability of selecting exactly 6 spades, 4 hearts, 2 diamonds, and 1 club is
`P=(^(13)C_(6)* ^(13)C_(4)* ^(13)C_(2)* ^(13)C_(1))/(^(52)C_(13))`.