Question

​(Inflation and interest rates​)​ You're considering an investment that you expect will produce a return of 8 percent next​ year, and you expect that your real rate of return on this investment will be 3 percent. What do you expect inflation to be next​ year?

Answer 1

The inflation rate is expected to be 4.8544% next year.

Step-by-step explanation:

The data we have on this problem is:

The nominal interest rate is 8%.

The real interest rate is 3%.

Knowing the formula for the real interest rate

`1+R = (1+r)/(1+i)`

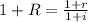
where R is the real interest rate, r is the nominal interest rate and i is the inflation rate, we can deduce the formula for the inflation rate as follows:

Step 1: multiply both members of the equation by (1+i)

`(1+R)(1+i)=1+r`

Step 2: divide both members of the equation by (1+R)

`1+i=((1+r))/((1+R))`

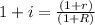
Step 3: substract 1 from both members of the equation

`i=((1+r))/((1+R)) - 1`

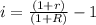
Step 4: replace the given values in the equation

`i=(1+0.08)/(1+0.03) -1=(108)/(103)-1 = 1.048544-1=0.048544`

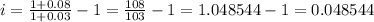
The inflation rate is expected to be 4.8544% next year.