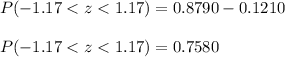Question

Find the area of the shaded region

Answer 1

Answer: Second Option

`P (-1.17 <z <1.17) = 0.7580`

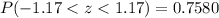
Explanation:

The shaded area corresponds to the interval

`-1.17 <z <1.17.`

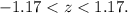
By definition, for a standard normal distribution the area under the curve in the interval (b <z <h) is equal to:

`P (b <z <h)`

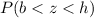
So in this case we look for:

`P (-1.17 <z <1.17)`

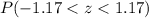
This is:

`P (-1.17 <z <1.17) = P (z <1.17) - P (z <-1.17)`

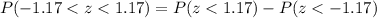
Looking at the standard normal table we have to:

`P (z <1.17) = 0.8790\\P (z <-1.17) = 0.1210`

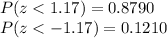
So:

`P (-1.17 <z <1.17) = 0.8790- 0.1210\\\\P (-1.17 <z <1.17) = 0.7580`