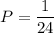Question

When four basketball players are about to have a​ free-throw competition, they often draw names out of a hat to randomly select the order in which they shoot. What is the probability that they shoot free throws in alphabetical​ order? Assume each player has a different name.

Answer 1

`P=(1)/(24)`

Explanation:

Let the names of 4 players start with letters A, B, C and D.

There is the the only chance that they shoot free throws in alphabetical​ order (ABCD).

Count how many different ways are to choose 4 letters from the hat. First letter can be chosen in 4 ways, the second letter can be chosen in 3 ways (only 3 letters left), the third letter can be chosen in 2 ways (only 2 letters left) and the fourth letter can be chosen in 1 way (the last letter left). So, there are

`4\cdot 3\cdot 2\cdot 1=24`

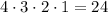
different orders.

The probability is

`P=(1)/(24)`