Question

Six different integers are picked from the numbers 1 through 10. How many possible combinations are there, if the the second smallest integer in the group is 3?

Please solve ASAP

Answer 1

1680 ways

Explanation:

We have to select 6 different integers from 1 to 10. It is given that second smallest integer is 3. This means, for the smallest most integer we have only two options i.e. it can be either 1 or 2.

So, the selection of 6 numbers would be like:

{1 or 2, 3, a, b, c ,d}

There are 2 ways to select the smallest digit. Only 1 way to select the second smallest digit. For the rest four digits which are represented by a,b,c,d we have 7 options. This means we can chose 4 digits from 7. Number of ways to chose 4 digits from 7 is calculated as 7P4 i.e. by using permutations.

`7P4 = (7!)/((7-4)!)=840`

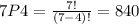
According to the fundamental rule of counting, the total number of ways would be the product of the individual number of ways we calculated above. So,

Total number of ways to pick 6 different integers according to the said criteria would be = 2 x 1 x 840 = 1680 ways