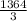Answer:
Sum =
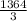
Explanation:
The given geometric sequence is:
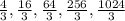
The first term of the sequence is
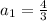
The common ratio of the sequence is:
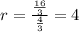
There are 5 terms in total in the given sequence so n = 5
The formula to calculate the sum of finite geometric sequence is:
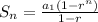
Using the given values, we get:
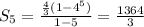
Therefore, the sum of given geometric sequence is