Question

A math teacher gives two different tests to measure students' aptitude for math. Scores on the first test are normally distributed with a mean of 23 and a standard deviation of 4.2. Scores on the second test are normally distributed with a mean of 71 and a standard deviation of 10.8. Assume that the two tests use different scales to measure the same aptitude. If a student scores 29 on the first test, what would be his equivalent score on the second test? (That is, find the score that would put him in the same percentile.)

84

86

77

87

Answer 1

86

Explanation:

Mean scores of first test =
`u_(1)=23`

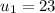
Standard deviation of first test scores =
`\sigma_(1) =4.2`

Mean scores of second test =
`u_(2)=71`

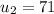
Standard deviation of second test scores =
`\sigma_(2) =10.8`

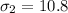
We have to find if a student scores 29 on his first test, what will be his equivalent score on the second test. The equivalent scores must have the same z-scores. So we have to find the z-score from 1st test and calculate how much scores in second test would result in that z-score.

The formula for z-score is:

`z=(x-u)/(\sigma)`

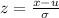
Calculating the z-score for the 29 scores in first test, we get:

`z=(29-23)/(4.2)=1.43`

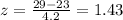
This means, the equivalent scores in second test must have the same z-scores.

i.e for second test:

`1.43=(x-71)/(10.8)\\\\ x-71 = 15.444\\\\ x = 86.444`

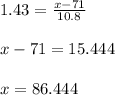
Rounding of to nearest integer, the equivalent scores in the second test would be 86.