Question

Find the mean and standard deviation of the probability distribution. Round answer to the nearest hundredth. Would it be unusual to have 3 defective computers in the batch? The probabilities that a batch of 4 computers will contain 0, 1, 2, 3, and 4 defective computers are 0.4096 , 0.4096 , 0.1536 , 0.0256 , and 0.0016 , respectively.

Answer 1

Mean = 0.8

Standard Deviation = 0.8

P(x = 3) is unusual event

Explanation:

Part A)

The probability distribution with correct formatting is shown in the table attached with:

We have to find the mean and standard deviation of this distribution. The mean of the probability distribution is calculated as summation of the products of "the variable with its respective probability".

`u = \sum x P(x)`

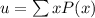
So, for the given distribution:

Mean = 0(0.4096) + 1(0.4096)+2(0.1536)+3(0.0256)+4(0.0016)

Mean = 0.8

Standard deviation is calculated by the following formula:

`\sigma=\sqrt{\sum x^(2)P(x) - u^(2)}`

`x^(2)P(x)=1.28`

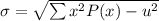
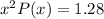
Substituting the values, we get:

`\sigma=\sqrt{1.28-(0.8)^(2)}\\\\ \sigma=0.8`

Part B)

Since the probability of 3 defective computers is less than 0.05, this is an unusual event.

So it would be unusual to have 3 defective computers in the batch.