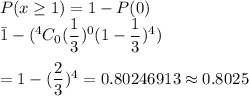Answer: 0.8025
Explanation:
Given : The number of defective calculators : 17
The number of calculators are not defective : 37
Total calculators : 37+17=54
The probability of the calculators are defective :
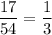
Binomial distribution formula :-
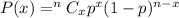 , where P(x) is the probability of success in x trials, n is total trials and p is the probability of success for one trial.
, where P(x) is the probability of success in x trials, n is total trials and p is the probability of success for one trial.
The probability that at least one of the calculators is defective is given by :-