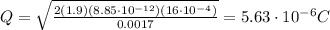Question

Two parallel plates that are initially uncharged are separated by 1.7 mm, have only air between them, and each have surface areas of 16 cm 2. How much charge must be transferred from one plate to the other if 1.9 J of energy are to be stored in the plates? (ε 0 = 8.85 × 10 -12 C 2/N ∙ m 2)

Answer 1

`5.63\cdot 10^(-6) C`

Step-by-step explanation:

The capacitor of a parallel-plate capacitor is given by:

`C=\epsilon_0 (A)/(d)`

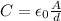
where

A is the area of each plate

d is the separation between the plates

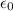`\epsilon_0` is the vacuum permittivity

The energy stored in a capacitor instead is given by

`U=(1)/(2)(Q^2)/(C)`

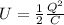
where

Q is the charge stored in each plate

Substituting the expression we found for C inside the last formula,

`U=(1)/(2)(Q^2 d)/(\epsilon_0 A)`

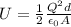
And re-arranging it

`Q=\sqrt{(2U\epsilon_0 A)/(d)}`

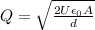
Now if we substitute

`d=1.7 mm=0.0017 m\\A=16 cm^2 = 16\cdot 10^(-4) m^2\\U = 1.9 J`

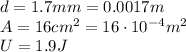
We find the charge stored on the capacitor:

`Q=\sqrt{(2(1.9)(8.85\cdot 10^(-12))(16\cdot 10^(-4)))/(0.0017)}=5.63\cdot 10^(-6) C`