Question

Simplify cos[arccsc((2/3)/3)].
A)no solution
B)sqrt3/2
C)1/2

Answer 1

1/2

Explanation:

We have
`\cos(\arccsc((2√(3))/(3)))`.

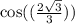Let
`u=\arccsc((2√(3))/(3))`.

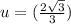This implies
`\csc(u)=(2√(3))/(3)`.

Use that sine and cosecant are reciprocals.

`\sin(u)=(3)/(2√(3))`

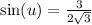
Now I'm going to rationalize the denominator there by multiply numerator and denominator by
`√(3)`:

`\sin(u)=(3√(3))/(2(3))`

`\sin(u)=(3√(3))/(6)`

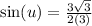
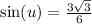
Reduce the fraction:

`\sin(u)=(√(3))/(2)`

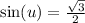
Now I'm going to use a Pythagorean Identity:
`\cos^2(u)+\sin^2(u)=1`.

This will give me the value of cos(u) which would give me the answer to my question if it exists.

Replace
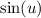`\sin(u)` with
`(√(3))/(2)` in:

`\cos^2(u)+\sin^2(u)=1`

`\cos^2(u)+((√(3))/(2))^2=1`

`\cos^2(u)+(3)/(4)=1`

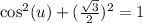
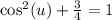
Subtract 3/4 on both sides:

`\cos^2(u)=(1)/(4)`

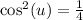
Square root both sides:

`\cos(u)=\pm (1)/(2)` (since 1/2*1/2=1/4 or -1/2*-1/2=1/4)

Now we must decide between the positive or the negative.

It depends where u lies. What quadrant? Hopefully it lays between 0 and
`\pi`. Otherwise, it doesn't exist (unless you have a different definition for arc function).

So u led to this equation earlier:

`\sin(u)=(√(3))/(2)`

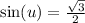
arcsin( ) only has outputs between
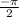`(-\pi)/(2)` and
`(\pi)/(2)`.

This would have to be in the first quadrant because we have only positive sine values there.

So this means cos(u)=1/2 and not -1/2 because we are using that u is in the 1st quadrant.

Remember u was
`\arccsc((2√(3))/(3))`.

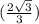So we have actually evaluated

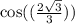`\cos(\arccsc((2√(3))/(3)))` without a calculator.

The value is 1/2.