Answers:
a) How high does the rock get?=1.933m
b)How far downrange from the pedestal does the rock land?=21.25m
Explanation:
This situation is a good example of projectile motion or parabolic motion, in which the travel of the rock has two components: x-component and y-component. Being their main equations as follows:
x-component:
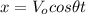 (1)
(1)
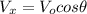 (2)
(2)
Where:
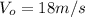 is the rock's initial speed
is the rock's initial speed
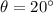 is the angle
is the angle
 is the time since the rock is propelled until it hits the ground
is the time since the rock is propelled until it hits the ground
y-component:
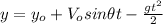 (3)
(3)
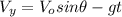 (4)
(4)
Where:
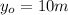 is the initial height of the rock
is the initial height of the rock
 is the final height of the rock (when it finally hits the ground)
is the final height of the rock (when it finally hits the ground)
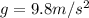 is the acceleration due gravity
is the acceleration due gravity
Knowing this, let's begin with the anwers:
a) How high does the rock get?
Here we are talking about the maximun height
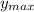 the rock has in its parabolic motion. This is fulfilled when
the rock has in its parabolic motion. This is fulfilled when
 .
.
Rewritting (4) with this condition:
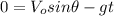 (5)
(5)
Isolating
 :
:
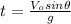 (6)
(6)
Substituting (6) in (3):
 (7)
(7)
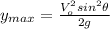 (8)
(8)
Solving:
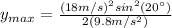 (9)
(9)
Then:
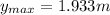 (10) This is the maximum height the rock has.
(10) This is the maximum height the rock has.
b) How far downrange from the pedestal does the rock land?
Here we are talking about the maximun horizontal distance
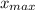 the rock has in its parabolic motion (this is fulfilled when
the rock has in its parabolic motion (this is fulfilled when
 ):
):
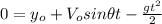 (11)
(11)
Isolating
 from (11):
from (11):
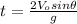 (12)
(12)
Substituting (12) in (1):
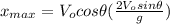 (13)
(13)
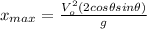 (14)
(14)
Knowing
 :
:
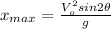 (15)
(15)
Solving:
 (16)
(16)
Finally:
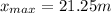 (17)
(17)