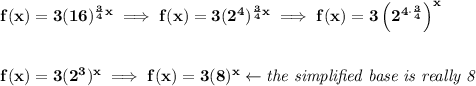Question

Which statement accurately describes the function f(x)=3(16)^3/4? Select three options

Answer 1

if we use a negative value for "x", our fraction becomes a negative exponent, small as it may be, meaning the 16, becomes a denominator, yielding a small amount however, is greater than 0.

if we use a positive value for "x", the 16 raised at that, yields still a value greater than 0.

if we use x = 0, the exponent turns to 0, 16⁰ = 1, and 3(1) = 3, meaning the initial value for f(x) is 3.

as you saw before, any negative "x" will give us a tiny number, but more than 0. Positive "x"s give us a larger value also more than 0, so f(x) or the range is really never going to be less than 0 but is > 0,

`\bf f(x)=3(16)^{(3)/(4)x}\implies f(x)=3(2^4)^{(3)/(4)x}\implies f(x)=3\left( 2^{4\cdot (3)/(4)} \right)^x \\\\\\ f(x) = 3(2^3)^x\implies f(x)=3(8)^x\leftarrow \textit{the simplified base is really 8}`