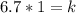Answer:
Part 1)
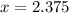
Part 2)
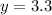
Part 3)

Explanation:
we know that
A relationship between two variables, x, and y, represent an inverse variation if it can be expressed in the form
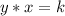 or
or
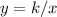
Part 1) y varies inversely with x. If y = 8 and k (the constant of variation) = 19, what is x?
we know that
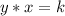
substitute the given values and solve for x
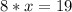
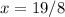
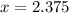
Part 2) y varies inversely with x, and k (the constant of variation) = 23. What is the value of y when x = 7?
we know that
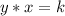
substitute the given values and solve for y
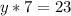

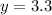
Part 3) y varies inversely with x. When y = 6.7, x = 1. What is the value of k, the constant of inverse variation?
we know that
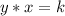
substitute the given values and solve for k