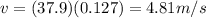Question

A woman is standing in the ocean, and she notices that after a wave crest passes by, five more crests pass in a time of 39.5 s. The distance between two successive crests is 37.9 m. What is the wave's (a) period, (b) frequency, (c) wavelength, and (d) speed?

Answer 1

(a) 7.9 s

The period of a wave is time that passes between two consecutive crests (or two consecutive troughs).

In this case, we are told that five crests pass in a time of 39.5 s. Therefore we can find the period by using the proportion:

`(5)/(39.5 s)=(1)/(T)`

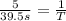
Where T is the period. Re-arranging the equation, we find

`T=((39.5)(1))/(5)=7.9 s`

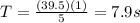
(b) 0.127 Hz

The frequency of a wave is equal to the reciprocal of the period:

`f=(1)/(T)`

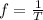
where

f is the frequency

T is the period

For this wave, we have T = 7.9 s, so its frequency is

`f=(1)/(7.9 s)=0.127 Hz`

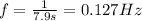
(c) 37.9 m

The wavelength of a wave is the distance between two consecutive crests (or two consecutive troughs). For this wave, the distance between two successive crests is 37.9 m, so the wavelength of the wave is

`\lambda=37.9 m`

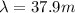
(d) 4.81 m/s

The speed of a wave is given by

`v=\lambda f`

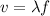
where

`\lambda` is the wavelength

f is the frequency

For the wave in the problem, we have

`\lambda=37.9 m\\f=0.127 Hz`

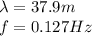
Therefore, the speed of the wave is

`v=(37.9)(0.127)=4.81 m/s`