Question

HELP ME!!!

Select the correct answer from the drop-down menu.

The value of x that satisfies the equation is °.

Answer 1

210 is the only choice I see listed that works.

Explanation:

I don't know if you know this but you can apply a co-function identity here giving you the equation:

`cos(x)=-(√(3))/(2)`.

If you are unsure of the identity sin(90-x)=cos(x) then I can show you another identity that leads to this one.

The difference identity for sine is sin(a-b)=sin(a)cos(b)-sin(b)cos(a).

Applying this to sin(90-x) gives you sin(90)cos(x)-sin(x)cos(90).

Let's simplify that using that sin(90)=1 while cos(90)=0:

sin(90-x)=sin(90)cos(x)-sin(x)cos(90)

sin(90-x)=1cos(x)-sin(x)(0)

sin(90-x)=cos(x)

You can also prove this identity using a right triangle like the one in this picture:

That missing angle is 90-x since we need the angles in this triangle to add up to 180 which it does:

(x)+(90)+(90-x)

x+90+90-x

x-x+90+90

0+180

180

Anyways you should see that sin(90-x)=b/c while cos(x)=b/c.

Since they are equal to the same ratio, then you can say sin(90-x)=cos(x).

There are other co-function identities you can get from using this idea.

Anyways back to the problem.

We are solving:

`cos(x)=-(√(3))/(2)`.

It looks like you have a drop-down menu with answers ranging from 0 to 360.

So I'm going to answer in degrees using the unit circle.

cosine value refers to the x-coordinate.

We are looking for when the x-coordinate is
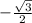`-(√(3))/(2)` which is at
`\theta=150^\circ , 210^\circ`.