Question

An advisor to the mayor of a large city wants to estimate, within 3 minutes, the mean travel time to work for all employees who work within the city limits. He knows that the standard deviation for all travel times is 12.25 minutes. He also wants to achieve a 95% confidence interval. He will poll a random sample of city employees. At least how many employees should he poll?

Answer 1

64

Explanation:

Given that an advisor to the mayor of a large city wants to estimate, within 3 minutes, the mean travel time to work for all employees who work within the city limits.

Let X be the random variable denoting the time for employees to travel within city limit

Std dev of X
`= 12.25 minutes`

For 95% confidence interval Z critical 1.96 is used because population std dev is known

Margin of error
`= 1.96*std error = 3 (given)`

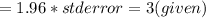
i.e.
`1.96((12.25)/(√(n) ) )=3`

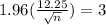
where n is the desired sample size.

Simplify to get

`(24.01)/(√(n) ) =3\\n=64.053`

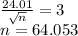
Hence atleast 64 employees should he poll