Question

Evaluate the function at the indicated values if possible. If an indicated value is not in the​ domain, say so.

f left parenthesis x right parenthesis equals StartFraction x plus 7 Over x squared minus 9 EndFraction
​; f left parenthesis negative 7 right parenthesis​, f left parenthesis 2 right parenthesis​, f left parenthesis 3 right parenthesis

Answer 1

f(-7)=0.

f(2)=-9/5.

f(3) doesn't exist because 3 isn't in the domain of the function.

Explanation:

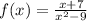`f(x)=(x+7)/(x^2-9)` is the given function.

We are asked to find:

`f(-7)`

`f(2)`

`f(3)`.

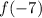
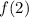
f(-7) means to replace x in the expression called f with -7:

Evaluate
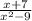`(x+7)/(x^2-9)` at
`x=-7`

`((-7)+7)/((-7)^2-9)`

`(0)/(49-9)`

`(0)/(40)`

`0`

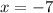
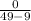
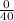
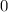
So f(-7)=0.

f(2) means to replace x in the expression called f with 2:

Evaluate
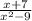`(x+7)/(x^2-9)` at
`x=2`

`(2+7)/(2^2-9)`

`(9)/(4-9)`

`(9)/(-5)`

`(-9)/(5)`

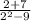
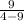
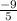
So f(2)=-9/5

f(3) means to replace x in the expression called f with 3:

Evaluate
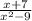`(x+7)/(x^2-9)` at
`x=3`

`(3+7)/(3^2-9)`

`(10)/(9-9)`

`(10)/(0)`

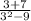
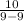
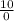
Division by 0 is not allowed so 3 is not in the domain of our function.