a. Factorize the denominator:
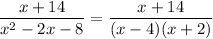
Then we're looking for
 such that
such that
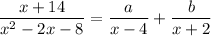
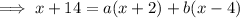
If
 , then
, then
 ; if
; if
 , then
, then
 . So we have
. So we have
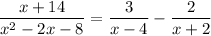
as required.
b. Same setup as in (a):

We want to find
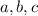 such that
such that
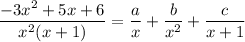
Quick aside: for the second term, since the denominator has degree 2, we should be looking for another constant
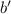 such that the numerator of the second term is
such that the numerator of the second term is
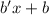 . We always want the polynomial in the numerator to have degree 1 less than the degree of the denominator. But we would end up determining
. We always want the polynomial in the numerator to have degree 1 less than the degree of the denominator. But we would end up determining
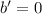 anyway.
anyway.

If
 , then
, then
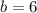 ; if
; if
 , then
, then
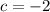 . Expanding everything on the right then gives
. Expanding everything on the right then gives
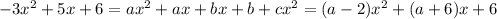
which tells us
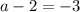 and
and
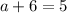 ; in both cases, we get
; in both cases, we get
 . Then
. Then
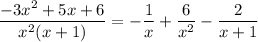
as required.