Question

Calculate the ratio of the resistance of 12.0 m of aluminum wire 2.5 mm in diameter, to 30.0 m of copper wire 1.6 mm in diameter. The resistivity of copper is 1.68×10−8Ω⋅m and the resistivity of aluminum is 2.65×10−8Ω⋅m.

Answer 1

Answer: 0.258

Step-by-step explanation:

The resistance
`R` of a wire is calculated by the following formula:

`R=\rho(l)/(s)` (1)

Where:

`\rho` is the resistivity of the material the wire is made of. For aluminium is
`\rho_(Al)=2.65(10)^(-8)m\Omega` and for copper is
`\rho_(Cu)=1.68(10)^(-8)m\Omega`

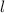`l` is the length of the wire, which in the case of aluminium is
`l_(Al)=12m`, and in the case of copper is
`l_(Cu)=30m`

`s` is the transversal area of the wire. In this case is a circumference for both wires, so we will use the formula of the area of the circumference:

`s=\pi{((d)/(2))}^(2)` (2) Where
`d` is the diameter of the circumference.

For aluminium wire the diameter is
`d_(Al)=2.5mm=0.0025m` and for copper is
`d_(Cu)=1.6mm=0.0016m`

So, in this problem we have two transversal areas:

For aluminium:

`s_(Al)=\pi{((d_(AL))/(2))}^(2)=\pi{((0.0025m)/(2))}^(2)`

`s_(Al)=0.000004908m^(2)` (3)

For copper:

`s_(Cu)=\pi{((d_(Cu))/(2))}^(2)=\pi{((0.0016m)/(2))}^(2)`

`s_(Cu)=0.00000201m^(2)` (4)

Now we have to calculate the resistance for each wire:

Aluminium wire:

`R_(Al)=2.65(10)^(-8)m\Omega(12m)/(0.000004908m^(2))` (5)

`R_(Al)=0.0647\Omega` (6) Resistance of aluminium wire

Copper wire:

`R_(Cu)=1.68(10)^(-8)m\Omega(30m)/(0.00000201m^(2))` (6)

`R_(Cu)=0.250\Omega` (7) Resistance of copper wire

At this point we are able to calculate the ratio of the resistance of both wires:

`Ratio=(R_(Al))/(R_(Cu))` (8)

`(R_(Al))/(R_(Cu))=(0.0647\Omega)/(0.250\Omega)` (9)

Finally:

`(R_(Al))/(R_(Cu))=0.258` This is the ratio