Question

A reflecting pool is shaped like a right triangle with one leg along the wall of a building. the hypotenuse is 9 feet longer than the side along the building. the third side is 7 feet longer than the side along the building. find the length of all three sides of the reflecting pool

Answer 1

Leg side along the wall = x ft = 8 ft

The other leg side = 7+x ft = 7+8=15 ft

The Hypotenuse =9+x ft = 9+8 = 17 ft

Explanation:

In the question, the shape of the pool is right triangle.

Let the leg side along the wall to be the x ft

Let the other leg side to be 7+x ft

Let the longest side/hypotenuse to be x+9 ft

Apply the Pythagorean relationship where the sum of squares of the legs equals the square of the hypotenuse

This means;

`x^2 +(x+7)^2=(x+9)^2\\\\`

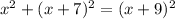
Expand the terms in brackets

`x^2+(x+7)^2=(x+9)^2\\\\\\x^2+x^2+14x+49=x^2+18x+81`

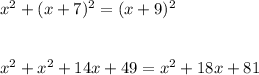
collect like terms

`x^2+x^2-x^2=18x-14x+81-49\\\\\\x^2=4x+32\\\\\\x^2-4x-32=0`

solve for x in the quadratic equation by factorization

`x^2-4x-32=0\\\\\\x^2-8x+4x-32=0\\\\\\x(x-8)+4(x-8)=0\\\\\\(x+4)(x-8)=0\\\\\\x+4=0,x=-4\\\\x-8=0,x=8`

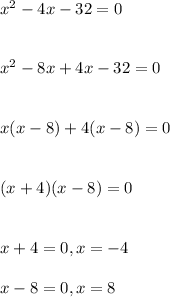
Taking the positive value of x;

x=8ft

Finding the lengths

Leg side along the wall = x ft = 8 ft

The other leg side = 7+x ft = 7+8=15 ft

The Hypotenuse =9+x ft = 9+8 = 17 ft