Question

Suppose we want a 90% confidence interval for the average amount spent on entertainment (movies, concerts, dates, etc.) by freshman in their first semester at a large university. The interval is to have a maximum bound on the error (or simply margin of error) of $2, and the amount spent has a normal distribution with a known standard deviation $30. The number of observations required is at least

Answer 1

609

Explanation:

Standard deviation =
`\sigma` = $30

Margin of error = E = $2

Confidence level = 90%

Since the distribution is said to be normal, we will use z scores to solve this problem.

The z score for 90% confidence level = z = 1.645

Sample size= n = ?

The formula to calculate the margin of error is:

`E=z(\sigma)/(√(n))\\\\√(n)=z(\sigma)/(E)\\\\n=((z\sigma)/(E) )^(2)`

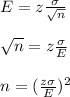
Using the values in above equation, we get:

`n=((1.645 * 30)/(2) )^(2)\\\\ n = 608.9`

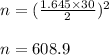
This means, the minimum number of observations required is 609