Question

When Mendel conducted his famous genetics experiments with peas, one sample of offspring consisted of 428 green peas and 155 yellow peas for a total of 583 peas. a) Find a 95% confidence interval estimate of the percentage of yellow peas and then interpret your answer.

Answer 1

(0.23, 0.30)

Explanation:

Number of green peas = 428

Number of yellow peas = 155

Total number of peas = n = 583

Since we have to establish the confidence interval for yellow peas, the sample proportion of yellow peas would be considered as success i.e. p =
`(155)/(583)`

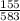
q = 1 - p =
`(428)/(583)`

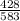
Confidence Level = 95%

Z value associated with this confidence level = z = 1.96

Confidence interval for the population proportion is calculated as:

`(p-z\sqrt{(pq)/(n)} ,p+z\sqrt{(pq)/(n)})`

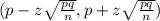
Using the values, we get:

`((155)/(583)-1.96\sqrt{((155)/(583) *(428)/(583))/(583) },(155)/(583)+1.96\sqrt{((155)/(583) *(428)/(583))/(583) })\\\\ =(0.23,0.30)`

Conclusion:

We are 95% confident that true value of population proportion of yellow peas lie between 0.23 and 0.30