Answer: 1.00
Step-by-step explanation:
The index of refraction
 is a number that describes how fast light propagates through a medium or material.
is a number that describes how fast light propagates through a medium or material.
Being its equation as follows:
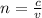 (1)
(1)
Where
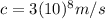 is the speed of light in vacuum and
is the speed of light in vacuum and
 its speed in the other medium and
its speed in the other medium and
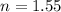 .
.
So, from (1) we can find the velocity at which the signal travels and then the time it requires to travel:
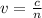 (2)
(2)
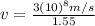 (3)
(3)
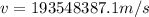 (4)
(4)
Now, knowing the velocity
 is the distance
is the distance
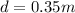 traveled in a time
traveled in a time
 :
:
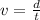 (5)
(5)
We can isolate
 from (5) and find the value of the required time:
from (5) and find the value of the required time:
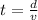 (6)
(6)
 (7)
(7)
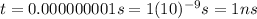 (8) This is the time it takes the signal to travel through the optical fiber: 1 nanosecond.
(8) This is the time it takes the signal to travel through the optical fiber: 1 nanosecond.