Question

What is the graph of the linear inequality 2x-3y<12

Answer 1

We understand a linear inequality as an inequality involving a linear function. It's important to know that a linear inequality contains one of the symbols of inequality:

< less than

> greater than

≤ less than or equal to

≥ greater than or equal to

In this problem, we have:

`2x-3y<12`

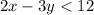
In this case, we use the symbol <, so this indicates that
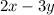`2x-3y` is less than 12. To solve this, let's write the linear equation in slope-intercept form:

Step 1: Write the expression as an equation:

`2x-3y=12`

Step 2: Subtract -2x from both sides:

`2x-3y-2x=12-2x \\ \\ -3y=12-2x`

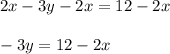
Step 3: Multiply the entire equation by -1/3

`-(1)/(3)(-3y)=-(1)/(3)(12-2x) \\ \\ y=(2)/(3)x-4`

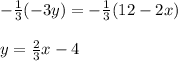
The graph of this equation is shown in the firs figure below. To know what's the shaded region let's take point (0, 0) and test it in the inequality:

`2(0)-3(0)<12 \\ \\ 0<12 \ TRUE!`

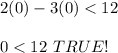
Since this is true, the shaded region includes point (0, 0) and this is above the graph. We have to draw a dotted line since equality is not included in the solution and this is shown in the second figure below.