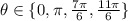Answer:
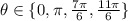
Explanation:
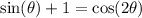
Applying double angle identity:
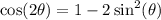
Doing so would give:
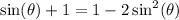
We need to get everything to one side so we have 0 on one side.
Subtract 1 on both sides:
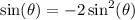
Add
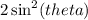 on both sides:
on both sides:
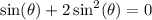
Let's factor the left-hand side.
The two terms on the left-hand side have a common factor of
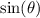 .
.
![\sin(\theta)[1+2\sin(\theta)]=0](https://img.qammunity.org/2020/formulas/mathematics/high-school/26do6yznbyk0sg6ed888j4c5teom1pny0l.png) .
.
This implies we have:
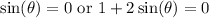 .
.
We need to solve both equations.
You are asking they be solved in the interval
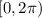 .
.
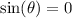
This means look at your unit circle and find when you have your y-coordinates is 0.
You this at 0 and
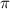 . (I didn't include
. (I didn't include
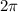 because you don't have a equal sign at the endpoint of
because you don't have a equal sign at the endpoint of
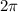 .
.
Now let's solve
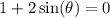
Subtract 1 on both sides:
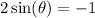
Divide both sides by 2:
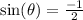
Now we are going to go and look for when the y-coordinates are -1/2.
This happens at
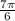 and
and
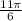 .
.
The solution set given the restrictions is