Answer:
0.372
Explanation:
Total number of attacks = n = 591
Number of critical strikes = x = 251
Proportion of critical strikes = p =
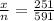
Proportion of non-critical strikes = q = 1 - p =

Confidence Level = 99%
Z-score for this confidence level = 2.58
The Lower bound for the population proportion is given by:
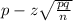
Using the values, we get:
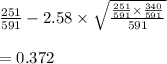
The lower bound for the 99% confidence interval for the proportion of strikes that are critical strikes is 0.372