Question

Suppose that in a lightning flash the potential difference between a cloud and the ground is 0.96×109 V and the quantity of charge transferred is 31 C. (a) What is the change in energy of that transferred charge? (b) If all the energy released could be used to accelerate a 950 kg car from rest, what would be its final speed?

Answer 1

(a)
`2.98\cdot 10^(10) J`

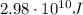
The change in energy of the transferred charge is given by:

`\Delta U = q \Delta V`

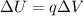
where

q is the charge transferred

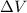`\Delta V` is the potential difference between the ground and the clouds

Here we have

`q=31 C`

`\Delta V = 0.96\cdot 10^9 V`

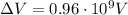
So the change in energy is

`\Delta U = (31 C)(0.96\cdot 10^9 V)=2.98\cdot 10^(10) J`

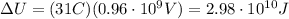
(b) 7921 m/s

If the energy released is used to accelerate the car from rest, than its final kinetic energy would be

`K=(1)/(2)mv^2`

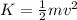
where

m = 950 kg is the mass of the car

v is the final speed of the car

Here the energy given to the car is

`K=2.98\cdot 10^(10) J`

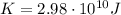
Therefore by re-arranging the equation, we find the final speed of the car:

`v=\sqrt{(2K)/(m)}=\sqrt{(2(2.98\cdot 10^(10)))/(950)}=7921 m/s`