Answer:
First problem: a (2,0)
Second problem: b. none of these; the answer is (4, 5/3) which is not listed.
Third problem: b. none of the above; there are no holes period.
Explanation:
First problem: The hole is going to make both the bottom and the top zero.
So I start at the bottom first.
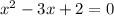
The left hand expression is factorable.
Since the coefficient of
 is 1, you are looking for two numbers that multiply to be 2 and add to be -3.
is 1, you are looking for two numbers that multiply to be 2 and add to be -3.
Those numbers are -2 and -1 since (-2)(-1)=2 and -2+(-1)=-3.
The factored form of the equation is:
 .
.
This means x-2=0 or x-1=0.
We have to solve both equations here.
x-2=0
Add 2 on both sides:
x=2
x-1=0
Add 1 on both sides:
x=1
Now to determine if x=2 or x=1 is a hole, we have to see if it makes the top 0.
If the top is zero when you replace in 2 for x, then x=2 is a hole.
If the top is zero when you replace in 1 for x, then x=1 is a hole.
Let's do that.
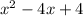
x=2
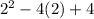
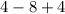
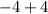
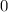
So we have a hole at x=2.
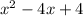
x=1
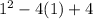
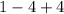
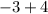

So x=1 is not a hole, it is a vertical asymptote. We know it is a vertical asymptote instead of a hole because the numerator wasn't 0 when we plugged in the x=1.
So anyways to find the point for which we have the hole, we will cancel out the factor that makes us have 0/0.
So let's factor the denominator now.
Since the coefficient of
 is 1, all we have to do is find two numbers that multiply to be 4 and add up to be -4.
is 1, all we have to do is find two numbers that multiply to be 4 and add up to be -4.
Those numbers are -2 and -2 because -2(-2)=4 and -2+(-2)=-4.
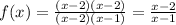
So now let's plug in 2 into the simplified version:
 .
.
So the hole is at x=2 and the point for which the hole is at is (2,0).
a. (2,0)
Problem 2:
So these quadratics are the same kind of the ones before. They all have coefficient of
 being 1.
being 1.
I'm going to start with the factored forms this time:
The factored form of
 is
is
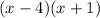 because -4(1)=-3 and -4+1=-3.
because -4(1)=-3 and -4+1=-3.
The factored form of
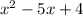 is
is
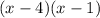 because -4(-1)=4 and -4+(-1)=-5.
because -4(-1)=4 and -4+(-1)=-5.
Look at
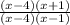 .
.
The hole is going to be when you have 0/0.
This happens at x=4 because x-4 is 0 when x=4.
The hole is at x=4.
Let's find the point now. It is (4,something).
So let's cancel out the (x-4)'s now.
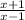
Plug in x=4 to find the corresponding y:
![(4+1)/(4-1){/tex]</p><p>[tex](5)/(3)](https://img.qammunity.org/2020/formulas/mathematics/high-school/xahohc9krb0cbdptcf2d39lgidjozfwetl.png)
The hole is at (4, 5/3).
Third problem:
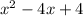 has factored form
has factored form
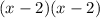 because (-2)(-2)=4 and -2+(-2)=-4.
because (-2)(-2)=4 and -2+(-2)=-4.
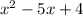 has factored form
has factored form
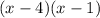 because (-4)(-1)=4 and -4+(-1)=-5.
because (-4)(-1)=4 and -4+(-1)=-5.
There are no common factors on top and bottom. You aren't going to have a hole. There is no value of x that gives you 0/0.