Question

A gun with a muzzle velocity of 100 m/s is fired horizontally from a tower. Neglecting air resistance, how far downrange will the bullet be 8 seconds later? g

Answer 1

313.6 m downward

Step-by-step explanation:

The distance covered by the bullet along the vertical direction can be calculated by using the equation of motion of a projectile along the y-axis.

In fact, we have:

`y(t) = h +u_y t + (1)/(2)at^2`

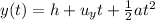
where

y(t) is the vertical position of the projectile at time t

h is the initial height of the projectile

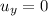`u_y = 0` is the initial vertical velocity of the projectile, which is zero since the bullet is fired horizontally

t is the time

a = g = -9.8 m/s^2 is the acceleration due to gravity

We can rewrite the equation as

`y(t)-h = (1)/(2)gt^2`

where the term on the left,
`y(t)-h`, represents the vertical displacement of the bullet. Substituting numbers and t = 8 s, we find

`y(t)-h= (1)/(2)(-9.8)(8)^2 = -313.6 m`

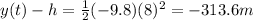
So the bullet has travelled 313.6 m downward.