Question

What is the range of f(x)= 5^x

Answer 1

The range is f(x) = all real values above 0.

In interval notation it is (0, ∞).

Explanation:

5^x can have any value above 0 . It cannot be negative or 0.

Answer 2

The range is
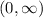`(0,\infty)` (in interval notation).

The range is
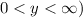`0<y<\infty)` or
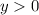`y>0` (in inequality notation).

The range is all real numbers greater than 0 (in words).

Explanation:

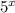`5^(x)` we get close to 0 but will never be 0.
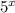`5^(x)` will also never be negative.

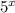`5^(x)` is positive for any real input
`x`.

Here is a table of values to help try to convince you we are only ever going to get positive outcomes.

`x` |
`5^x`

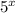
-4 5^(-4)=1/625

-3 5^(-3)=1/125

-2 5^(-2)=1/25

-1 5^(-1)=1/5

0 5^0=1

1 5^1=5

2 5^2=25

3 5^3=125

4 5^4=625

You can see the y's are increasing as you increase the x value.

Even if you plug in really left numbers on the number like -200 you will still get a positive number like
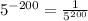`5^(-200)=(1)/(5^(200))`. This number will be really close to 0. You can go more left of -200 and the outcome will be even closer to 0.

I'm just trying to convince you on the left side the y's will approach 0 but never cross the x-axis on the right side the numbers keep getting larger and larger.

The range is
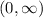`(0,\infty)` (in interval notation).

The range is
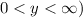`0<y<\infty)` or
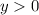`y>0` (in inequality notation).

The range is all real numbers greater than 0 (in words).

You can also look at the graph and see that the y's for this equation only exist for number y's greater than 0. You only see the graph above the x-axis.