Question

Suppose your company needs $13 million to build a new assembly line. Your target debt-equity ratio is .55. The flotation cost for new equity is 6 percent, but the flotation cost for debt is only 3 percent. Your boss has decided to fund the project by borrowing money because the flotation costs are lower and the needed funds are relatively small. a. What is your company’s weighted average flotation cost, assuming all equity is raised externally? (Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.) b. What is the true cost of building the new assembly line after taking flotation costs into account? (Do not round intermediate calculations and enter your answer in dollars, not millions, rounded to the nearest whole dollar amount, e.g., 1,234,5667.)

Answer 1

Answer:True cost =
`(cost of assembly)/(1-weighted flotation cost )`

=
`(13,000,000)/(1- 0.049)`

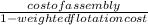
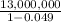
= $ 13,669,821.2

Step-by-step explanation:

Given :

Debt-Equity ratio = 0.55

Flotation cost for new equity = 6%

Flotation cost for debt = 3 %

∴ To compute the weighted flotation cost , we'll use the following formula:

Weighted Flotation cost =
`\left [ (1)/(1+Debt-Equity ratio)* Flotation cost of equity \right ] + \left [ (Debt-Equity ratio)/(1+Debt-Equity ratio)* Flotation cost of debt \right ]`

=
`\left [ (1)/(1+0.55)* 0.06 \right ] + \left [ (0.55)/(1+0.55)* 0.03 \right ]`

= 0.0387 + 0.0106

= 0.04934 or 4.93%

The true cost of building the new assembly line after taking flotation costs into account is evaluated using the following formula :

True cost =
`(cost of assembly)/(1-weighted flotation cost )`

=
`(13,000,000)/(1- 0.049)`

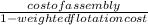
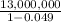
= $ 13,669,821.2