Answer:
rd+premium = 10.5%
using CAPM = 10.3%
Step-by-step explanation:
Under bond-yield+ risk-premium approach
This method simply propose to add the bond yield with the estmated risk premium:
0.065 + 0.04 risk premium = 0.105
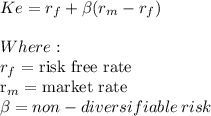
r_f = 0.055
β = 0.8
(r_m-r_f) = 0.06
0.055 + 0.8(0.06) = 0.103 cost of capital using CAPM